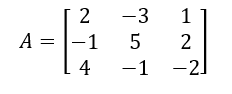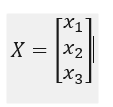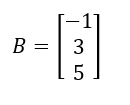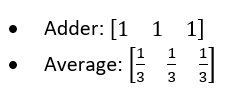Is Linear Algebra Hard?
Linear algebra is a critical field of mathematics that you must master to venture into machine learning. As important as the study is, it is equally hard. So what exactly makes linear algebra hard? We’ll find that out in this article along with tips on how to make linear algebra easier.
The fact is linear algebra is a field with numerous esoteric findings and theories. Still, the notations and tools about nuts and bolts derived from the area are useful for those working in machine learning. For this reason, linear algebra is known as the mathematics of data.
The field primarily deals with linear combinations wherein you use arithmetic on different columns and arrays of numbers called “vectors” and “matrices”, to create different columns and arrays consisting of numbers. You study lines, planes, vector spaces, and mappings in linear needed for linear transforms.
Digging Deeper into Linear Algebra
Linear algebra is a relatively young branch of mathematics, formalized during the 1800s to discover the unknown things related to linear equations. When studying advanced linear algebra, it is important to brush up on your knowledge of linear equations quickly.
So what is a linear equation?
A linear equation is mainly a series of mathematical operations and terms wherein some terms are unidentified. Here is an example of a linear equation:
Such equations define a line that exists on a two-dimensional plane. The line is formed by adding some random values into the unspecified “x” to determine how the model/ equation affects the value of “y.”
You can come up with an entire system of linear equations based on the same format with one, two, or even more unknowns such as shown below:
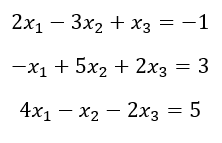
“Data columns” are the columns that contain the coefficients. It is treated as matrix A.
The variables and form a vector of the unknowns, X, that you need to solve.
You can represent the column vector of outputs as B:
Compactly, you can express the linear algebra notation in the following manner:
The unknowns or variables:
can be calculated as:
Most people don’t have a hard time with linear equations, but linear algebra makes matters trickier.
Is Linear Algebra A Hard Subject?
Many students regard linear algebra as a difficult study. It is more challenging than discrete mathematics which is usually a first-year program taught in most STEM majors. Linear algebra is taught in its second year and demands robust reasoning and analytical skills.
When it comes to the different levels of mathematics, linear algebra ranks at the “intermediate level,” but is quite tough, similar to calculus II. That said, there are many other advanced courses like topology and abstract algebra.
Customarily, it is a good idea to have a thorough understanding of calculus I before starting your linear algebra journey. It is also mandatory for studying upper-level, advanced mathematics programs.
To cap it, linear algebra is complex for sure, but you can manage the difficulty you go through. If you repeatedly work on the problem sets, practice them regularly, and analyze equations logically, your understanding of the subject improves and deepens with time. It is also a wise approach to read more linear algebra textbooks.
Elements of Linear Algebra that Make It Challenging

You may be wondering now what makes linear algebra so tough?
Simply put, the answer is that the field is not quite intuitive. It levies a sound emphasis on having rigorous proofs constantly. Moreover, the fundamentals of linear algebra are abstract which makes it somewhat problematic for you to visualize them. You cannot really picture a linear algebra equation on a graph on your head, and cannot see it going through fluctuations to yield different results. Since there is hardly any clear visualization, the concepts are difficult to grasp and practice.
In addition, linear algebra contrasts from the majority of the high school and college programs and courses. Mostly, mathematics students visualize the mathematical functions in graphical terms. Since it is the chief math course, you can graph all the mathematics taught before linear algebra on a leaf of your notebook.
On the other hand, you have to accept algebraic manipulations that steer you away from direct visualization forms in linear algebra. You need to modify and align your understanding of mathematics to comprehend the perplexing and non-concrete algebraic material in linear algebra.
Some of the most challenging elements in linear algebra include: defining mathematical structures using a set of axions, wrapping your head around eigenvectors, and grasping the concepts of abstract vector space and linear independence.
Difficulty in linear algebra also arises because you first need to understand terms and different definitions. Once you are through with that step, determine the kind of calculation and the specific analysis to apply to get the required outcome. This is a complicated step for most students which adds to the complexity of linear algebra.
Many abstract concepts form the basics of the study that are quite demanding. Before you start studying linear algebra, you need to focus on calculation instead of comprehending the concepts and terms. After that, you move on to the assessment of different calculations you need to use.
Students often struggle to write proofs that reinforce the difficulty level of linear algebra. You may not find it hard at the start as it is rather straightforward in the beginning. However, the study becomes incredibly complex as you progress, especially when you have covered its basics.
Typically, there is no involvement of calculus in linear algebra basics. Still, as you delve into advanced mathematics, you come across linear algebraic problems that demand an understanding of calculus and vice versa. This interconnection exists in linear algebra and in many other dimensions of mathematics. You will discover calculus dipped in physics, economics, and statistics. Similarly, numerical analysis, topology, optimization, and trigonometry have many overlapping concepts.
Students often compare the difficulty level of linear algebra to that of calculus. The truth is that linear algebra is less complicated than elementary calculus. On the contrary, it is sometimes difficult to excel in calculus despite having excellent knowledge of theorems. Once you understand the different theorems in linear algebra, you can easily solve different questions.
As hard as linear algebra is, you become quite comfortable with calculus and its different operations once you are familiar with it. Algebra helps you easily grasp topics in calculus.
After going through the challenging aspects of linear algebra, let’s focus on some tactics to simplify it.
Adopt an Intuitive Approach Towards Linear Algebra

Usually, it becomes difficult to grasp a concept because we perceive it as something hard and do not dig deeper into its meaning. Many students similarly treat linear algebra. Instead of adopting a hostile attitude towards it, let us decipher its meaning. Once you do that, perceive it with an intuitive approach, and you will be amazed at how it becomes interesting for you.
Learn to Organize Operations and Inputs
Courses smack you down with details related to matrices. If only you learn to organize the inputs and operations, the problem will become easier. Understand it in this way:
- You have a group of inputs you need to track
- You have to perform predictable linear operations
- You generate an output, in the end, transforming it again probably
First, you need to know how to track some inputs. Why not simplify it with a list:
- x
- y
- z
You could also write it as (x, y, z).
Now you need to focus on tracking the operations. Remember, you have “mini arithmetic,” which means there will be multiplications with a constant and an addition in the end. If the operation “F” acts like this:
F (x, y, z) = 2x + 3y + 4z
You can abbreviate the function as (2, 3, 4). You know you have to multiply the first input with the first value, second input with second value, and third input with third value, and then add up the results.
If you only consider the first input:
G (x, y, z) = 2x + 0y + z = (2, 0, 1)
Let us make it a wee bit more interesting: how to handle many sets of inputs simultaneously? If you want to run the operation F on (a, b, c) as well as (x, y, z) at the same time, you can try this:
F (a, b, c, x, y, z) = ?
This, however won’t work: F expects 3 inputs at one time, not 6. It would help if you separated all the inputs in groups:
|
1st Input |
2nd Input |
|
A |
x |
|
B |
y |
|
C |
z |
Looks much neater now!
How can you run the same input via numerous operations? It would be best if you had a row for every operation:
- F: 2 3 4
- G: 2 0 1
You are getting quite organized now: inputs lie in vertical columns with operations residing in horizontal rows.
Picture the Matrix
In addition to using these strategies, remember to visualize a matrix too. To picture a matrix, you need to envision the inputs, operations, and then the outputs:
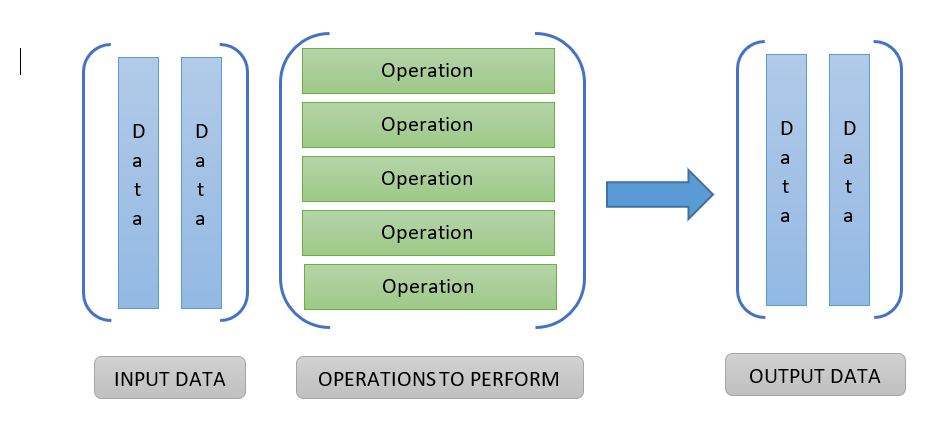
Imagine that you pour every input through every operation to get an output:
When an input passes through an operation, it creates an output item. In the example above, the input (a, b, c) moves against the operation F, and outputs as:
It moves against the G operation and outputs:
Solving a complex set of linear equations can be made easy with the help of linear Algebra. Transform the data vector to an identity matrix using matrix operations, and the values of the unknown variables reveal at the output side.
Let’s Work on Some Fancy Linear Algebra Operations
Operations can be quite tough in linear algebra. Let us simplify them today. Assume that you have 3 inputs, you can easily whip up some 1-operation matrices:
The ‘adder’ is basically a + b + c.
The ‘average’ is more similar to:
Now try these easy one liners:
Now let us combine them in a single matrix:
Wow! It is the “identity matrix” right that copies 3 inputs right to 3 outputs.
Now let us take a look at this:
The inputs are reordered so (x,y,z) turns to (x,z,y).
And take another look at this one:
This one right above is an input doubler.
You could rewrite it as 2.1 (the identity matrix) too. when you treat the inputs like vector coordinates, the operations matrix changes to vectors.
- Scale makes inputs smaller or bigger
- Skew makes some inputs smaller or bigger
- Rotate makes fresh coordinates based on existing ones
- Flip turns inputs into negative
These geometric interpretations of multiplication also help you warp vector spaces; don’t forget that the vectors are basically examples of the data you must modify.
Practice and Practice Some More!
We want you to overcome your troubles with linear algebra. If you use the approaches we have discussed above and sincerely practice them for some time daily, you will gradually find yourself warming up to the field.
Honestly, it isn’t all that tough. Your approach towards the subject is what makes it easy or difficult. See it from a new angle, and you will successfully grasp the concepts in linear algebra. We are here to help you throughout the process.