High School Math
Homework Help & Tutoring
We offer an array of different online High School Math tutors, all of whom are advanced in their fields and highly qualified to instruct you.
High School Math
Solving Inequalities
Take a look at this interesting math problem:
Solve (2x-9)(x-4) ≥ 0
For this inequality to have a value that is greater or equal to 0, it is also necessary for the product of both parts of the equation (the values in parenthesis) to be 0 or greater. This is possible in two cases:
1) Both sets of parentheses equate to 0 or more, as the product of the two values that are greater or equal to 0 is also always greater than or equal to 0, or -
2) Similarly, both sets of parentheses equate to less than or equal to 0, as the product of two negative or zero values is also always greater than or equal to 0.
Consequently the final result is the result of either case, but what is interesting here is that the final result is the union of the outcome of both cases, and at the same time (during the solving of the individual cases) both values must be greater or equal to 0 (per case 1) or less or equal to 0 (case 2). Let's look at the above example:
Case 1:
2x-9 ≥ 0 and x-4 ≥ 0
We have a value, x, that is greater than or equal to 9/2 and also a value of x that is greater than or equal to 4. The final result therefore is x ≥ 9/2
Case 2:
2x-9 ≤ 0 and x-4 ≤ 0
X is equal to or less than 9/2; x-4 is equal to less than 4. Therefore the final result is x ≤ 4
This means the solution to the problem example is either of these results: x ≤ 4 or x ≥ 9/2.
The Number Pi
Background
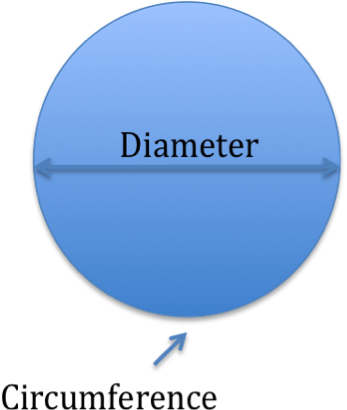
Those of you who have done maths at high school level or higher have encountered the special number called pi or π a few times. Whenever you want to calculate the circumference or area of a circle, it is used in the well-known formulas¹:
Circumference = pi * Diameter
Area = pi * Radius * Radius
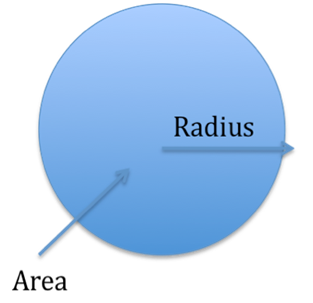
It also appears in a number of other formulas, such as the volume of a sphere.
History
The earliest accounts of the number for pi appear to be from the Babylon culture, around 1900 – 1680 BC² . Scientists measuring the diameter and the circumference and the diameter realised that the quota between them was always the same, they got 3.125. The Egyptians and other early cultures then made advancements in the approximations, but it was not until the great Archimedes of Greece ∼287-212 BC, that the real breakthrough came. He used great trigonometric skills² to get it right within 99.9 % .
In 1761, it was proven by a Swiss mathematician that the number is irrational, i.e. the number of decimals are infinite³. This era also provided the name from the 16th letter in the Greek alphabet, π. The title was given by fellow great scientist and maths expert Leonhard Euler.
Number of digits
3,1415 and then, how many digits can you remember? Modern day computers have been able to calculate it up to 12 trillion digits, but the record, according to Guinness Book of Records, for a human stands at 67890, set by someone in China in 2005.
Pronunciation
There is a bit of discussion as to how the letter pi should be pronounced. The Greek sound is like ”pee”, but the English language uses the i sound as in ”pie”. Most other languages have stuck to the original Greek version 4 .
Further reading:
If this has sparked your interest in the intricacies of pi, I would recommend A History of Pi from Czech-American Petr Beckmann6. That should give you a much more comprehensive understanding of the importance of this ”magical” number.
References:
[1] http://www.mathgoodies.com/lessons/vol2/circumference.html
[2] http://www.livescience.com/29197-what-is-pi.html
[3] http://en.wikipedia.org/wiki/Pi
[5] http://www.eveandersson.com/pi/books
[6] Beckmann, Petr: A history of Pi. Golam Press, 1970.
To fulfill our tutoring mission of online education, our college homework help and online tutoring centers are standing by 24/7, ready to assist college students who need homework help with all aspects of high school math. Our high school subjects tutors can help with all your projects, large or small, and we challenge you to find better online high school math tutoring anywhere.
College High School Math Homework Help
Since we have tutors in all High School Math related topics, we can provide a range of different services. Our online High School Math tutors will:
- Provide specific insight for homework assignments.
- Review broad conceptual ideas and chapters.
- Simplify complex topics into digestible pieces of information.
- Answer any High School Math related questions.
- Tailor instruction to fit your style of learning.
With these capabilities, our college High School Math tutors will give you the tools you need to gain a comprehensive knowledge of High School Math you can use in future courses.
24HourAnswers Online High School Math Tutors
Our tutors are just as dedicated to your success in class as you are, so they are available around the clock to assist you with questions, homework, exam preparation and any High School Math related assignments you need extra help completing.
In addition to gaining access to highly qualified tutors, you'll also strengthen your confidence level in the classroom when you work with us. This newfound confidence will allow you to apply your High School Math knowledge in future courses and keep your education progressing smoothly.
Because our college High School Math tutors are fully remote, seeking their help is easy. Rather than spend valuable time trying to find a local High School Math tutor you can trust, just call on our tutors whenever you need them without any conflicting schedules getting in the way.






