Chaos Theory
Homework Help & Tutoring
We offer an array of different online Chaos Theory tutors, all of whom are advanced in their fields and highly qualified to instruct you.
Chaos Theory
Snow Crystals, Fractals and Self Similarity
Introduction
The pieces of snow falling to the ground in winter have two very special scientific characteristics:
- No two flakes are exactly alike
- If you cut one, the remaining portions will have the same shape as what you cut from
These amazing qualities have been studied in the realm of Chaos Theory.
Uniqueness
According to a renowned scientist, finding two identical snowflakes is like ”shuffling a deck of cards and getting the exact same shuffle back. You could shuffle every second for the entire life of the universe, and you wouldn’t come close to getting two of the same”.1 In order to explain this, we must look at the way that snow crystals are formed.
As snow is water, the basic blocks are in the majority of molecules two hydrogen atoms and one oxygen atom. While the atoms are all alike, about 1 in 5000 molecules2 will be a so called ”heavy water” or ”deuterium oxide” compound, where the hydrogen atoms are the 2H isotope3 with two particles (one proton + one neutron) in the nucleus instead of the normal 1H isotope.
These abberrations are placed at random points in the lattice. And since there are some 1018 atoms in a normal snowflake, about 1014 – 1015 deuterium molecules will be placed at some locations in the atomic structure.2 The likelihood of two different configurations of such a high number being exactly the same is so low that it can be considered impossible!2
Self Similarity
The classical example of a system with self similarity is the Babushka or Matryoshka doll.4 When opening it, a doll with the exact shape and look comes out, only smaller, and this keeps repeating. The mathematical definition of this is a fractal, and this has been observed and used in many early cultural art forms.5
Snow is not perfectly self similar, but a mathematical fractal is like snow to a degree of 95-99 %.6,7 It has been shown in a model of how snowflakes are formed that they indeed take a shape given by a fractal pattern.8
The Koch snowflake
Swedish researcher Helge von Koch used fractal theory to build figures of snowflakes as early as 1904. The process was to start with a triangle and then continuously split each side and add another triangle at the half point. This yielded the initial sequence of shapes shown in Figure 1.
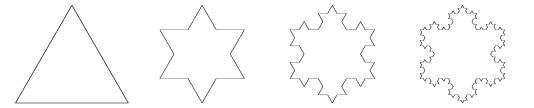
Figure 1. Four first Koch snowflakes [9].
References
[1] Prof. Kenneth Libbrecht, Californa Institute of Technology, quote from PBS Newshour.
[2] http://www.its.caltech.edu/~atomic/snowcrystals/alike/alike.htm - Snowflakes - No Two Alike? Caltech.
[3] http://pubchem.ncbi.nlm.nih.gov/compound/deuterium_oxide - Open Chemistry Database.
[4] https://en.wikipedia.org/wiki/Matryoshka_doll - Wikipedia.
[5] http://polynomial.me.uk/2009/09/20/fractals-of-brain-fractals-of-mind/ - Self Similarity ~ Fractals, Fractals Everywhere, Karl Richard 2009.
[6] Fractals – A Brief Explanation. Junior University, available through http://juni.osfc.ac.uk/Aim_Higher/Maths/
[7] Prof. Craig A. Tovey, Georgia Institue of Technology, answered on http://www.researchgate.net/post/Are_snowflakes_based_on_fractal_geometry .
[8] Nittmann, J. and Stanley, H.E.: Non-deterministic approach to anisotropic growth patterns with continuously tunable morphology: the fractal properties of some real snowflakes, Journal of Physics A, vol. 20, Number 17, also available at http://iopscience.iop.org/0305-4470/20/17/010
[9]. http://mathworld.wolfram.com/KochSnowflake.html - Wolfram MathWorld.
To fulfill our tutoring mission of online education, our college homework help and online tutoring centers are standing by 24/7, ready to assist college students who need homework help with all aspects of chaos theory. Our physics tutors can help with all your projects, large or small, and we challenge you to find better online chaos theory tutoring anywhere.
College Chaos Theory Homework Help
Since we have tutors in all Chaos Theory related topics, we can provide a range of different services. Our online Chaos Theory tutors will:
- Provide specific insight for homework assignments.
- Review broad conceptual ideas and chapters.
- Simplify complex topics into digestible pieces of information.
- Answer any Chaos Theory related questions.
- Tailor instruction to fit your style of learning.
With these capabilities, our college Chaos Theory tutors will give you the tools you need to gain a comprehensive knowledge of Chaos Theory you can use in future courses.
24HourAnswers Online Chaos Theory Tutors
Our tutors are just as dedicated to your success in class as you are, so they are available around the clock to assist you with questions, homework, exam preparation and any Chaos Theory related assignments you need extra help completing.
In addition to gaining access to highly qualified tutors, you'll also strengthen your confidence level in the classroom when you work with us. This newfound confidence will allow you to apply your Chaos Theory knowledge in future courses and keep your education progressing smoothly.
Because our college Chaos Theory tutors are fully remote, seeking their help is easy. Rather than spend valuable time trying to find a local Chaos Theory tutor you can trust, just call on our tutors whenever you need them without any conflicting schedules getting in the way.





