Quantum Physics
Homework Help & Tutoring
We offer an array of different online Quantum Physics tutors, all of whom are advanced in their fields and highly qualified to instruct you.
Quantum Physics
If quantum cosmologists can reconcile quantum mechanics with Einstein's Theory of General Relativity, we may be in for a wild ride, as scientists will finally have a single theory with the potential to describe all aspects of time and space in the universe. In short, we will be on our way to knowing the unknowable. Quite exciting, to say the least. At the heart of quantum theory lies such ideas as the particle nature of waves, the wave-like properties of particles, the quantized energy levels of atoms, and the Heisenberg Uncertainty Principle. It is from these fundamental assumptions about the natural world that we may be able to unlock its secrets through the development of a unified field theory. A good course in quantum physics will take students through the following areas:
- The wave function
- Time-independent Schrodinger equation
- Formalism
- Quantum mechanics in three dimensions
- Identical particles
- Time-independent perturbation theory
- The variational principle
- The WKB approximation
- Time-dependent perturbation theory
- The adiabatic approximation
- Scattering
There are plenty of books on quantum physics to be found on Google and Amazon.com. There is also a nice collection of books and journals devoted to this area which students can find at the Springer website.
The variational principle
If a quantum system has a Hamiltonian independent of time and one chooses a normalized “well behaved” function (i.e. a continuous function for which the first and second derivatives exist) then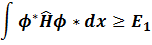
where 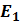 is the lowest energy eigenvalue of the Hamiltonian (bound energy).
is the lowest energy eigenvalue of the Hamiltonian (bound energy).
In other words, if we chose a random test function 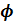 the bounded energy will be minimum of the expression
the bounded energy will be minimum of the expression 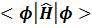
Question 1
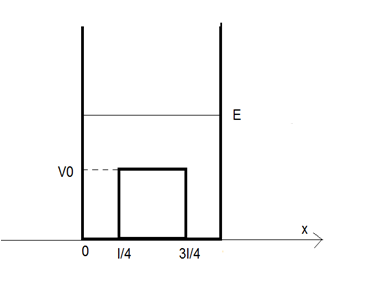
Consider a one-dimensional system of a particle with a potential energy:
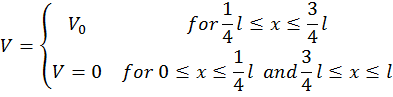
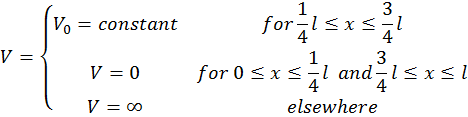
Make a graph of V vs X. Use the test function 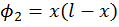 to determine the energy of the ground level. Note that there is no variational parameter. Note that
to determine the energy of the ground level. Note that there is no variational parameter. Note that 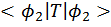 is given by the equation (why?):
is given by the equation (why?):
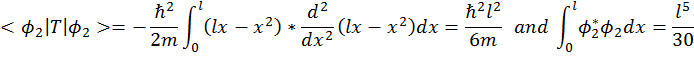
Solution:
If you consider a test function 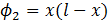 having no variational parameter (that is having no constant coefficients inside) then the eigenvalue of the bound level can be approximated by
having no variational parameter (that is having no constant coefficients inside) then the eigenvalue of the bound level can be approximated by
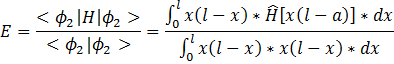
Since
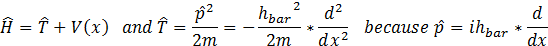
We can write:
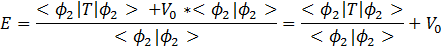
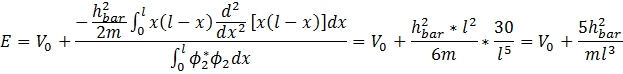
since we have:
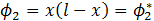
Question 2
Consider you have a test function:
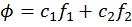
where f1 and f2 are real functions. Find the energy of the bound level in terms of the integrals
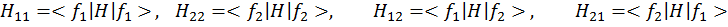
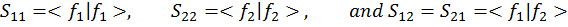
For the special case when:
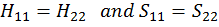
find also the rapport of the coefficients: 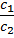
Solution:
If you have a test function of the type
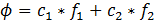
Then the energy of the bound level is given by (like above):
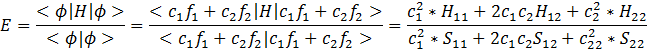
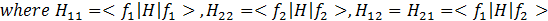
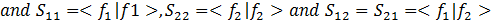
Which for:
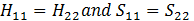
gives the rapport of coefficients:
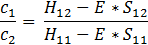
To have a solution of the above system of two equations one needs to have the characteristic determinant = 0. In other words the condition for existence of E states is:
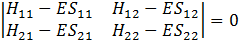
or
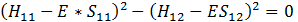
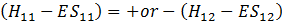
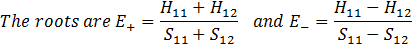
To fulfill our tutoring mission of online education, our college homework help and online tutoring centers are standing by 24/7, ready to assist college students who need homework help with all aspects of quantum physics. Our physics tutors can help with all your projects, large or small, and we challenge you to find better online quantum physics tutoring anywhere.
College Quantum Physics Homework Help
Since we have tutors in all Quantum Physics related topics, we can provide a range of different services. Our online Quantum Physics tutors will:
- Provide specific insight for homework assignments.
- Review broad conceptual ideas and chapters.
- Simplify complex topics into digestible pieces of information.
- Answer any Quantum Physics related questions.
- Tailor instruction to fit your style of learning.
With these capabilities, our college Quantum Physics tutors will give you the tools you need to gain a comprehensive knowledge of Quantum Physics you can use in future courses.
24HourAnswers Online Quantum Physics Tutors
Our tutors are just as dedicated to your success in class as you are, so they are available around the clock to assist you with questions, homework, exam preparation and any Quantum Physics related assignments you need extra help completing.
In addition to gaining access to highly qualified tutors, you'll also strengthen your confidence level in the classroom when you work with us. This newfound confidence will allow you to apply your Quantum Physics knowledge in future courses and keep your education progressing smoothly.
Because our college Quantum Physics tutors are fully remote, seeking their help is easy. Rather than spend valuable time trying to find a local Quantum Physics tutor you can trust, just call on our tutors whenever you need them without any conflicting schedules getting in the way.






