Mathematical Physics

Mathematical physics is the powerful tool that physicists and chemists use in their everyday research to predict the real life systems using abstract mathematical models. Using the equations of mathematical physics you can calculate an enormous amount of different systems – starting from a guitar string and ending with the radioactive activity of a specific element! Both of these real world systems are explained with partial differential equations.

In this article, this is the easiest example that exists in mathematical physics –  the derivation of the string equation, and on this example you will be able to notice the basic considerations of mathematical physics.

So, the string, as shown on the picture, will be a mathematical model.

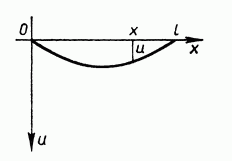
First of all, we need to list the major approximations – we neglect width and height of the string, to be able to concentrate on length.  In addition, we will say that the string is absolutely flexible, which means that there is no resistance to any external force that bends the string.

So, as you see on the picture, we have a string with a length l. We say that there are tension forces T in the x direction and that the ends of the string are fixed.

To finish mathematical modeling we say that every point of the string moves in a direction orthogonal to the x axis; these oscillations are small and that string is homogeneous.

Since the oscillations are small the law of the oscillation can be given as a function of 2 variables:  , where u, as shown on the picture is the distance of a point on the string at coordinate x at time t from the x axis.

Now, we use the formula for an arc length to show, that at the time t:

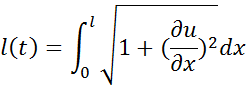
We already stated that   is small. If the string is smooth enough, the derivative  is small as well. Hence, when we square this derivative, it will have a value with a higher order of infinitesimal. We will assume that these oscillations are so small that we neglect the derivative. Hence, the length of a string is:

That simply means that including small oscillations of the string, we consider the length to be constant. From the same considerations, any given part of a string will have constant length.

From the given assumptions about the characteristics of oscillations, we can get the next conclusions: since the length of the string is constant, the tension at any given point will be constant and be equal to T. Then we can see that  , where  is the angle between tangent and a string in point x and the time t (recall this formula from pre-calculus). So, we can derive: 

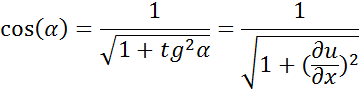
However, from our assumption, we neglect the square of the derivative. So, at any given point of the string we have: 

From here we can start the derivation of the equation for the oscillation of a string. For this we take into consideration a small part of the string given by x and  . Since we assumed that the string is homogeneous the density is constant, and we will denote it as . Then the mass of this part of the string will be equal to . On two sides of this part of the string we have forces acting on it. They are equal in magnitude     (), and opposite in direction.

The horizontal component of these forces is equal to zero

The vertical component will be given as:

Now we have:

which means that vertical component can be rewritten as:

From Lagrange theorem we can say that 

where c is an arbitrary point that lies inside x and . Now, applying Newton’s second law,  ,  , and remembering that acceleration is second derivative of distance by time, we can state that:

If we cancel x and state that  is infinitesimal. Then c will be close to x and we will get: 

Finally, if we denote  , we obtain the final result for a string equation: 

This is a partial differential equation that completely describes the movement of a string. Amazingly, the same equation will be used if we want to know the thermal conductivity of a beam. There are multiple ways to solve these equations like separation of variables, or the Dirichlet method. If you would like to learn more about this topic, or if you have any other problem in mathematical physics, we will gladly help you!

You can read more about partial differential equations at MIT Open Courseware, and a useful set of notes on mathematical physics can be found here.

To fulfill our tutoring mission of online education, our college homework help and online tutoring centers are standing by 24/7, ready to assist college students who need homework help with all aspects of mathematical physics. Our physics tutors can help with all your projects, large or small, and we challenge you to find better online mathematical physics tutoring anywhere.